 vectors,
vectors, 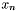 , where each
, where each 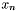 has three components. As the molecular conformation changes, therefore, the result is a new set of vectors
has three components. As the molecular conformation changes, therefore, the result is a new set of vectors 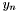 . We can capture the the differences between conformations using these two sets of vectors.
. We can capture the the differences between conformations using these two sets of vectors.If it's your day job to push proteins in silico then you will one day have to calculate the RMSD of a protein. For example, you've just simulated the protein GinormousA for a whole micro-second, but you don't even know if GinormousA is stable. Sure, you could load up a protein viewer and eyeball the stability of the protein throughout the simulation. But eye-balling is just not going to cut it with your boss -- you need to slap a number on it. This is where RMSD comes in. RMSD is a quantitative measurement of difference between two atomic structures.
A molecule's conformation is basically a set of 3-dimensional coordinates. This means that a conformation is a set of  vectors,
vectors, 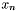 , where each
, where each 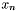 has three components. As the molecular conformation changes, therefore, the result is a new set of vectors
has three components. As the molecular conformation changes, therefore, the result is a new set of vectors 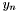 . We can capture the the differences between conformations using these two sets of vectors.
. We can capture the the differences between conformations using these two sets of vectors.
To make life easier, we first shift the center of mass of 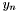 and
and 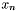 to the origin of the coordinate system (we can always shift them back afterwards). Once "centered," the differences between the vector sets can be captured by the total squared distance between them:
to the origin of the coordinate system (we can always shift them back afterwards). Once "centered," the differences between the vector sets can be captured by the total squared distance between them:
![\[ E = \sum_n{|x_n - y_n|^2} \]](form_3.png)
The root mean-square deviation (RMSD) is then:
![\[ RMSD = \sqrt{\frac{E}{N}} \]](form_4.png)
But hola, you say...this mean-square measure doesn't measure similarity very well! After all, any rotation of the set of 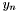 (which doesn't change the internal arrangement of
(which doesn't change the internal arrangement of 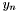 ), would distort the RMSD! What we really need, then, is to find the best rotation of
), would distort the RMSD! What we really need, then, is to find the best rotation of 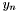 with respect to
with respect to 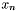 before taking the RMSD. To rotate the vectors
before taking the RMSD. To rotate the vectors 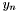 , we apply a rotation matrix
, we apply a rotation matrix 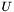 to get
to get 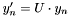 . We can then express
. We can then express 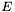 as a function of the rotation
as a function of the rotation 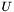 :
:
![\[ E = \sum_n{|x_n - U \cdot y_n|^2} \]](form_8.png)
Thus, to find the RMSD, we must first find the rotation 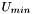 that minimizes
that minimizes 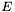 -- the optimal superposition of the two structures.
-- the optimal superposition of the two structures.
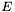 to get this rotation. The algorithm described in those papers have since become part of the staple diet of protein analysis. As the original proof for the Kabsch equations (using 6 different Lagrange multipliers) is rather tedious, we'll describe a much simpler proof using standard linear algebra.
to get this rotation. The algorithm described in those papers have since become part of the staple diet of protein analysis. As the original proof for the Kabsch equations (using 6 different Lagrange multipliers) is rather tedious, we'll describe a much simpler proof using standard linear algebra.
First, we expand 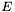 (which is now a function of
(which is now a function of 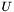 ):
):
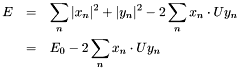
The first part, 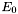 , is invariant with respect to a rotation
, is invariant with respect to a rotation 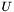 . The variation resides in the last term,
. The variation resides in the last term, 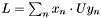 . The goal, therefore, is to find the matrix
. The goal, therefore, is to find the matrix 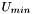 that gives the largest possible value of
that gives the largest possible value of 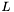 , from which we obtain:
, from which we obtain:
![\[ RMSD = \sqrt{\frac{E_{min}}{N}} = \sqrt{\frac{E_0 - 2 \cdot L_{max}}{N}} \]](form_14.png)
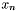 and
and 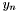 into two
into two 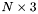 matrices
matrices 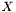 and
and 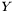 . Then we can write
. Then we can write 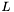 as a matrix trace:
as a matrix trace:
![\[ L = Tr( X^T U Y ) \]](form_18.png)
where 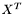 is a
is a 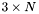 matrix and
matrix and 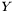 is an
is an 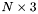 matrix. Juggling the matrices inside the trace, we get:
matrix. Juggling the matrices inside the trace, we get:
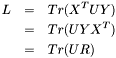
Now, we still don't know what 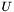 is, but we can study the matrix
is, but we can study the matrix 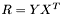 , which is the
, which is the 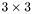 correlation matrix between
correlation matrix between 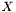 and
and 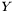 . Furthermore, by invoking the powerful Singular Value Decomposition theorem, we know that we can always write R as:
. Furthermore, by invoking the powerful Singular Value Decomposition theorem, we know that we can always write R as:
![\[ R = V S W \]](form_24.png)
and obtain the 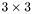 matrices
matrices 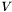 and
and 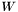 (which are orthogonal), and
(which are orthogonal), and 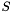 (which is positive diagonal, with elements
(which is positive diagonal, with elements 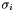 ). We can then substitute these matrices into the expression for
). We can then substitute these matrices into the expression for 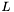 :
:
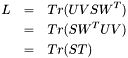
Because 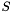 is diagonal, we can get a simple expression for
is diagonal, we can get a simple expression for 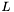 in terms of the
in terms of the 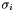 :
:
![\[ L = Tr( S T ) = \sigma_1 \cdot T_{11} + \sigma_2 \cdot T_{22} + \sigma_3 \cdot T_{33} \]](form_30.png)
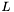 . The secret sauce is in
. The secret sauce is in 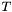 . If we look at the definition of
. If we look at the definition of 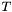 , we can see that it is a product of orthogonal matrices, namely, the matrices
, we can see that it is a product of orthogonal matrices, namely, the matrices 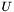 ,
, 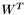 and
and 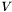 . Thus,
. Thus, 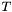 must also be orthogonal.
must also be orthogonal.
Given this, the largest possible value for any element of 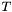 is 1, or
is 1, or 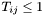 . And since
. And since 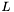 is a product of terms linear in the diagonal elements of
is a product of terms linear in the diagonal elements of 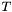 , the maximum value of
, the maximum value of 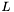 occurs when the
occurs when the 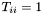 :
:
![\[ L_{max} = Tr( S T_{max} ) = \sigma_1 + \sigma_2 + \sigma_3 = Tr( S ) \]](form_35.png)
Plugging this into the equation for RMSD, we get
![\[ RMSD = \sqrt{ \frac{E_0 - 2 (\sigma_1 + \sigma_2 + \sigma_3 )}{N} } \]](form_36.png)
From this analysis, we can also determine the rotation that yields the optimal superposition of the vectors. When 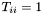 , then
, then 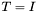 , the identity matrix. This immediately gives us an equation for the optimal rotation
, the identity matrix. This immediately gives us an equation for the optimal rotation 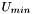 in terms of the left and right orthogonal vectors of the matrix R:
in terms of the left and right orthogonal vectors of the matrix R:
![\[ T_{max} = W^T U_{min} V = I \]](form_38.png)
![\[ U_{min} = W V^T \]](form_39.png)
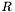 , but we still don't know how to find them! Never fear. Kabsch, who first derived the solution, showed that to solve for
, but we still don't know how to find them! Never fear. Kabsch, who first derived the solution, showed that to solve for 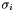 , we should solve the matrix
, we should solve the matrix 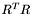 , which is a nice symmetric real matrix, and is consequently much easier to solve. Expanding on the singular value decomposition from the previous section
, which is a nice symmetric real matrix, and is consequently much easier to solve. Expanding on the singular value decomposition from the previous section
![\[ R^TR = (W^T S^T V^T)(V S W) = W^T S^2 W \]](form_42.png)
we can see that the singular value term of 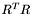 is
is 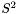 . In other words, the singular values of
. In other words, the singular values of 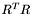 (
(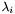 ) are related to the singular values of
) are related to the singular values of 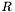 (
(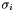 ) by the relationship
) by the relationship 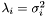 . And also, the right singular vectors
. And also, the right singular vectors 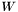 are the same for both
are the same for both 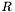 and
and 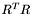 .
.
Furthermore, since 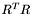 is a symmetric real matrix, its eigenvalues are identical to its singular values
is a symmetric real matrix, its eigenvalues are identical to its singular values 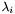 . Thus, we can use any standard method (e.g. the Jacobi transformation) to find the eigenvalues of
. Thus, we can use any standard method (e.g. the Jacobi transformation) to find the eigenvalues of 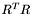 , and by substituting
, and by substituting 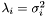 into the RMSD formula:
into the RMSD formula:
![\[ RMSD = \sqrt { \frac{ E_0 - 2 ( \sqrt{\lambda_1} + \sqrt{\lambda_2} + \sqrt{\lambda_3} )}{N} } \]](form_46.png)
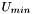 from the SVD theorem. You see,
from the SVD theorem. You see, 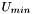 is guaranteed to be orthogonal, but for our RMSD calculation, we don't just want orthogonal matrices, we want rotation matrices. And while orthogonal matrices can have determinants of +1 or -1, "proper" rotation matrices have determinants of +1 (unless they're also reflected, in which case they'll have determinants of -1, and are termed "improper" rotations).
is guaranteed to be orthogonal, but for our RMSD calculation, we don't just want orthogonal matrices, we want rotation matrices. And while orthogonal matrices can have determinants of +1 or -1, "proper" rotation matrices have determinants of +1 (unless they're also reflected, in which case they'll have determinants of -1, and are termed "improper" rotations).When does this happen? To answer this question, take a look at your hands. Assuming that you're a primate, you have two of them, both alike, but reflected across the plane of symmetry that runs down the center of your body. Now, try to superimpose your hands. Go ahead. Try. If you're observant, you'll notice that you simply can't superimpose your hands. Even if you cut them off of your arms, the best you can hope to do is to align them so that their outlines are coincident -- but the palm of one hand will still be touching the other. You can never perfectly superimpose your hands, because your hands are chiral.
The same thing happens in molecular systems -- molecules are frequently chiral, and when two molecules are related by chirality, it sometimes happens that their optimal superposition involves a rotation, followed by a reflection. Thus, the "improper" rotation. Unfortunately, a reflection in 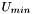 will result in an incorrect RMSD value using the stated algorithm, so we need to detect this situation before it becomes a problem.
will result in an incorrect RMSD value using the stated algorithm, so we need to detect this situation before it becomes a problem.
To restrict the solutions of 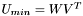 to proper rotations, we check the determinants of
to proper rotations, we check the determinants of 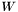 and
and 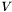 :
:
![\[ \omega = det( V ) \cdot det( W ) \]](form_48.png)
If 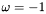 then there is a reflection in
then there is a reflection in 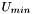 , and we must eliminate the reflection. The easiest way to do this is to reflect the smallest principal axis in
, and we must eliminate the reflection. The easiest way to do this is to reflect the smallest principal axis in 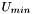 , by reversing the sign of the third (smallest) eignevalue, which yields the final Kabsch formula for RMSD in terms of
, by reversing the sign of the third (smallest) eignevalue, which yields the final Kabsch formula for RMSD in terms of 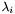 and
and 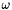 :
:
![\[ RMSD = \sqrt { \frac{ E_0 - 2 ( \sqrt{\lambda_1} + \sqrt{\lambda_2} + \omega \sqrt{\lambda_3} )}{N} } \]](form_51.png)
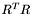 , rather than using an iterative approach (such as Jacobi). If only RMSD is desired (i.e. the calculation of a rotation matrix is unecessary), the get_rmsd() method is more efficient.
, rather than using an iterative approach (such as Jacobi). If only RMSD is desired (i.e. the calculation of a rotation matrix is unecessary), the get_rmsd() method is more efficient.In addition to these methods, a get_trivial_rmsd() function is provided to calculate the RMSD value between two structures without attempting to superimpose their atoms.
 1.5.1
1.5.1