BTK Core: gyration

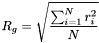
Formally, the radius of gyration relates any N-dimensional collection of particles to an N-dimensional sphere with an equivalent moment of inertia and axis of rotation (in other words, it maps a irregular object to a sphere that will rotate the same way.) In structural biology, this is primarily useful because it is an metric for the average size, or "compacness," of a molecule.

For our purposes we'll use a slightly simpler formalism -- the radius of gyration of a molecule is the root-mean-square distance of every atom in the molecule from the molecule's geometric center:

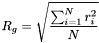
where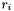

is the distance of atom $i$

from the molecule's center, and $N$

is the number of atoms in the molecule. This isn't the exact physical definition of the radius of gyration, but it works for our purposes, because the individual atomic masses rarely influence the result of the calculation.

In order to calculate this quantity from a structure, we need to load the structure from a file (in this case, a PDB file), and to do that we need to define a few basic types:

00001 typedef BTK::ATOMS::PDBAtom atom;
00001 typedef BTK::MOLECULES::Monomer<atom> monomer;
00002 typedef BTK::MOLECULES::Polymer<monomer> polymer;
00003 typedef BTK::IO::PDBSystem<polymer> pdb_system;

00001   pdb_system pdb(filename);

A PDBSystem is actually just a BTK::MOLECULES::System object, with the adiitional ability to parse a Protein Data Bank (PDB) structure file. In this example, we use the default behavior of the class -- it loads every chain in a PDB file, and stores them in separate Polymer chains.

Once loaded, we could use a PDBSystem to iterate over the chains in a PDB file, and then iterate over the atoms in those chains (i.e. a nested loop), but in this example, we'll make use of the ability of the PDBSystem to iterate over every atom in a loaded structure:

00001   BTK::MATH::BTKVector gc = 
00002     BTK::ALGORITHMS::geometric_center(pdb.structure_begin(),
00003                                       pdb.structure_end());

Here we've called the geometric_center template function, which takes two AtomIterator objects that define a range of atoms, and calculates the unweighted geometric center of their positions. We then use this point to calculate the sum of squared radii for every atom in the structure:

00001   pdb_system::atom_iterator ai;
00002   double sum_rg_squared = 0.0;
00003   unsigned N = 0;
00004 
00005   for (ai = pdb.structure_begin(); ai != pdb.structure_end(); ++ai) {
00006     double r = BTK::MATH::length(ai->position() - gc); // r == distance
00007     sum_rg_squared += r * r;  // keep a running sum of the distance squared
00008     ++N; // count the number of atoms
00009   }

Again, we've relied upon the ability of the PDBSystem to iterate over every atom in the structure, as if they were part of a single chain. This greatly simplifies the code, as it isn't necessary to write multiple nested loops to iterate through all of the atoms in a system of polymers. Instead, we write a single, concise loop that does exactly what we need.

In this case, we have used an atom_iterator from the PDBSystem class to step through every atom in the loaded structure, and using some BTK::MATH functions, we've calulated the length (r) of the vector from the geometric center of the molecule to each atom's position. We then squared this value, and kept a running sum of the squared radii, in addition to a count of the total number of atoms in the PDBSystem (note that we could have called num_atoms() on the PDBSystem to get this value outside of the loop, if we didn't care about the extra cost of counting atoms).

Now that we have a sum of squared radii, calculation of the gyration radius of the molecule is absolutely trivial:

00001   std::cout << "radius of gyration: " 
00002             << std::sqrt(sum_rg_squared / N) << std::endl;

Here we calculate the mean squared radius (rum_rg_squared/N), and take the square root of the resulting value to obtain the gyration radius. We were able to write this (admittedly simple) application in less than 15 minutes, and in fewer than 60 lines of code, including comments. Not bad for an application that loads and parses a PDB file, does a non-trivial calculation, and produces a scientifically-useful result!

For reference, here's the complete source code for this example (which can be found in examples/gyration_radius.cpp):

00001 // -*- mode: c++; indent-tabs-mode: nil; -*-
00002 //
00003 //The Biomolecule Toolkit (BTK) is a C++ library for use in the
00004 //modeling, analysis, and design of biological macromolecules.
00005 //Copyright (C) 2006, Tim Robertson <kid50@users.sourceforge.net>
00006 //
00007 //This program is free software; you can redistribute it and/or modify
00008 //it under the terms of the GNU Lesser General Public License as published
00009 //by the Free Software Foundation; either version 2.1 of the License, or (at
00010 //your option) any later version.
00011 //
00012 //This program is distributed in the hope that it will be useful,  but
00013 //WITHOUT ANY WARRANTY; without even the implied warranty of
00014 //MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
00015 //Lesser General Public License for more details.
00016 //
00017 //You should have received a copy of the GNU Lesser General Public License
00018 //along with this program; if not, write to the Free Software Foundation,
00019 //Inc., 59 Temple Place - Suite 330, Boston, MA  02111-1307, USA.
00020 
00021 #include <iostream>
00022 #include <string>
00023 #include <cmath>
00024 
00025 #include <btk/core/math/vector_math.hpp>
00026 #include <btk/core/atoms/pdb_atom.hpp>
00027 #include <btk/core/molecules/monomer.hpp>
00028 #include <btk/core/molecules/polymer.hpp>
00029 #include <btk/core/io/pdb_system.hpp>
00030 #include <btk/core/algorithms/properties.hpp>
00031 
00032 typedef BTK::ATOMS::PDBAtom atom;
00033 typedef BTK::MOLECULES::Monomer<atom> monomer;
00034 typedef BTK::MOLECULES::Polymer<monomer> polymer;
00035 typedef BTK::IO::PDBSystem<polymer> pdb_system;
00036 
00037 int main(int argc, char * argv[])
00038 {
00039   std::string filename;
00040 
00041   if (argc == 2) {
00042     filename = argv[1];
00043   } else {
00044     std::cerr << "usage: " << argv[0]
00045               << " <pdb filename>"
00046               << std::endl;
00047     return -1;
00048   }
00049   
00050   // load the PDB file
00051   pdb_system pdb(filename);
00052 
00053   // calculate the geometric center of all atoms in the PDB file
00054   BTK::MATH::BTKVector gc = 
00055     BTK::ALGORITHMS::geometric_center(pdb.structure_begin(),
00056                                       pdb.structure_end());
00057 
00058   // iterate through every atom in the PDB file, and calculate its
00059   // distance from the geometric center of the molecule
00060   pdb_system::atom_iterator ai;
00061   double sum_rg_squared = 0.0;
00062   unsigned N = 0;
00063 
00064   for (ai = pdb.structure_begin(); ai != pdb.structure_end(); ++ai) {
00065     double r = BTK::MATH::length(ai->position() - gc); // r == distance
00066     sum_rg_squared += r * r;  // keep a running sum of the distance squared
00067     ++N; // count the number of atoms
00068   }
00069   
00070   std::cout << "radius of gyration: " 
00071             << std::sqrt(sum_rg_squared / N) << std::endl;
00072   
00073   return 0;
00074 }